フェルミ推定とは、実際に調査することが難しい数値などを最低限の情報・知識から論理的に概算することを指します。例えば、「日本にある電柱の数を算出せよ」というような問題が出され、この問いに対して既定の時間内で結論を出すことが求められます。

＊ケース問題との違いについては別の記事「ケース面接って何？〜評価されるポイントと対策方法〜」で説明しています。

次に、フェルミ推定をどのように解き進めればよいのか、基本的な枠組みをご紹介します。

大きな方針としては、まず求めたい数値を求めるための式を作ります。例えば先程の「日本にある電柱の数を算出せよ」という問題では、

日本にある電柱の数＝日本の国土面積 × 平地の割合 × 一定面積当たりの電柱の数

というような式を作ることができます。

それから、国土面積、面積当たりの電柱の数などそれぞれの因子の値を推測していきます。例えば面積当たりの電柱の本数ならば、「自分の家の周囲〇〇メートル四方にだいたい〇〇本の電柱がある」などを思い浮かべ、それらしい数値を計算によって導き出します。

ここで気づいた方もいるかもしれませんが、フェルミ推定を解くためにはあらかじめ知っておかなければならない数値も存在します。ここでは国土面積や平地の割合がそれに当たります。

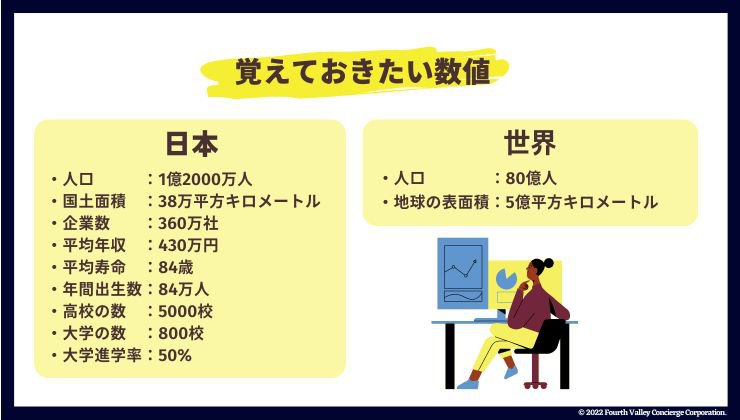
フェルミ推定の対策をするにあたって、以下の数値を覚えておく事をおすすめします。

それでは実際に例題を解いてみましょう。一問目は難易度を比較的低めにしています。

例題①：「今年の日本全国における大学受験生の人数を求めよ」

解法：

まず今年の大学受験生の人数を求める式は以下の通りになります。

今年の大学受験者数＝①同年齢の子どもの人数 × ②高校進学率 × ③大学進学率

（以上現役受験生の人数） ＋ ④浪人受験生の人数

ではそれぞれの要素について大まかな数値を当てはめていきましょう。

①同年齢の子どもの人数

；1年に生まれる子どもの数と同じなので、約85万人

②全国の高校進学率

；100%（99%）と仮定

③全国の大学進学率（現役受験生のみとする）

；50%

④浪人受験生の人数

；全国の高校の１学年（②より、約85万人）で、浪人受験を選択する割合を10%と仮定

①～③までの計算式

850,000 × 1 × 0.5 =425,000 …(A)

④の計算式

850,000 × 0.1=85,000...(B)

よって

(A)+(B)=425,000+85,000=510,000

以上より、今年の日本全国における大学受験生の人数はおよそ51万人と推測できます。


―――――
例題②：ファミレスの年間市場規模

解法：

次に国内のファミレスの年間市場規模を推測してみましょう。

式は以下の通りになります。

ファミレスの年間市場規模 = ①利用人口（リピーター） × ②顧客単価 × ③年間来店回数

①ファミレスを利用する人口

ファミレスの顧客は固定的であり、売り上げの多くはリピーター客によるものです。そのため今回は対象をリピーター層に絞り、計算を行います。

10歳以下の子どもがいる家庭と、65歳以上の定年退職を迎えた高齢者が主なリピーターであると考えると、ファミレスを定期的に利用する人数は以下のように求められます。

・10歳以下の子どもがいる家族世帯の総人口

ー10歳以下が850万人（1年に生まれる子どもが85万人より）

ー平均出生率は1.5人

→8,500,000 ÷ 1.5 ≒ 600万世帯

ー世帯平均人数が3.5だとすると、総人口は約2000万人

・65歳以上の総人口

ー65歳以上は総人口の約30%

→120,000,000 × 0.3＝4000万人

よってリピーター層の条件にあてはまるのは全部で6000万人となり、そのうちの50%がファミレスを定期的に利用すると仮定すると、ファミレスを定期的に利用する人口は3000万人となります。

②顧客単価

ランチ（朝〜夕方）が1000円、ディナーが1500円、そしてディナー利用率が全体の7割だと仮定します。

③年間平均来店回数

月に2回、年に24回来店すると仮定します。

以上をもとに計算を行うと

( 30,000,000 × 0.3 × 1000 + 30,000,000 × 0.7 × 1500 ) × 24

= ( 9,000,000,000 + 31,500,000,000 ) × 24

= 約9600億円

と推測できます。

実際の面接では、例題②のような問題を５分前後という短い制限時間内で解くことが求められるので、どこまで掘り下げて考えるかの判断やタイムマネジメントが重要になります。

また立式の際の要素の細分化も、必ずしも細かくすればいいというわけではない点に注意が必要です。例えば例題①で求めた「今年の日本全国における大学受験生の人数」には、就職後に再度学び直したいと考えた、学生ではない大人の受験生も実際には含まれています。しかし学生の受験生に比べるとかなり少数であり、導き出される数値に大きな差は生じないと考えられるため、今回の場合は考慮する必要はありません。

フェルミ推定で最も重要なのは、「答えを導き出すプロセスが論理的かどうか」です。導き出した数値が正確であるに越したことはありませんが、数値の正確さにこだわりすぎるあまり時間内に解ききることができない、考慮すべき要素を全て網羅できないとならないようにしましょう。

フェルミ推定上達にはとにかく慣れが重要です。今回紹介したような例題を、本番を想定してじっくり解くことが最も効果的ですが、電車の中など、腰を据えてフェルミ推定に取り組めないというようなときは、頭の中で立式を行うだけでも十分効果的です。